Inhaltsverzeichnis
Falls es irgendweche Rückfragen gibt, so schreibe man diese an mailto:esa@fsmpi.rwth-aachen.de!
If there are any additional questions, please send an email to mailto:esa@fsmpi.rwth-aachen.de!
Auf dieser Seite mögen sich alle Menschen eintragen, die beim Projekttag Physik 2012 (Freitag, der 5.10.) Experimente betreuen.
In this Wiki, all tutors who are helping at the „Projekttag Physik 2012“ (Friday, 5th of October) shall register.
Die gelb gehighlighteten Versuche sind dabei nur von Mitarbeitern aus dem Physikzentrum zu besetzen, da es sich hier um „gefährliche“ Versuche handelt, für die die Betreuer sinnvoller Weise Erfahrung oder sogar eine Unterweisung in die Nutzung der Materialien vorweisen können sollten.
The yellow highlighted experiments are somehow „dangerous“ and thus, shall only be overseen by „professionals“ from the RWTH physics department.
Schichtenplan / Time Slots
(Versuchsbeschreibungen s. unten.)
(Experiment descriptions see below)
| Time | hole in coin (2 people wished), Room 26 C 201 | interference with hair (2 people wished), Room: 26 C 401 | pendulum (2 people wished), Room: 26 C 402 | balloon rocket, Room: 28 B 110 | water rocket Place: In front of building 28 (southern door, floor 0) | Torricelli's law, Place: In the back of building 28, floor 1, main door (next to the big lecture hall) | bridge and ship, Room: MBP 026 | Band generator, Room: MBP 015 |
|---|---|---|---|---|---|---|---|---|
| 10:00 - 10:30 | Jan-Michael Mol and Rob McNeil | Olivier De Castro & Rita Fabry | Pascal Späing & Andreas Albert | Adrian | Joel Schumacher & Jan Grahe | Sebastian Hanfland | Christian Ritzer | Christoph Gordalla |
| 10:30 - 11:00 | Jan-Michael Mol and Rob McNeil | Olivier De Castro & Rita Fabry | Pascal Späing & Andreas Albert | Adrian | Joel Schumacher & Jan Grahe | Sebastian Hanfland | Christian Ritzer | Christoph Gordalla |
| 11:00 - 11:30 | Jan-Michael Mol and Rob McNeil | Olivier De Castro & Rita Fabry | Pascal Späing & Andreas Albert | Adrian | Christoph Gordalla | Sebastian Hanfland | Sebastian Schaub | Theo Glauch und Max Mahlke |
| 11:30 - 12:00 | Jan-Michael Mol and Rob McNeil | Olivier De Castro & Rita Fabry | Pascal Späing & Andreas Albert | Adrian | Christoph Gordalla | Sebastian Hanfland | Sebastian Schaub | Theo Glauch und Max Mahlke |
| 12:00 - 12:30 | Barbara Hohenbichler and Rob McNeil | Markus Scheb & Rita Fabry | Daniel Otten und Tobias Hoelzer | Marc Joosten | Theo Glauch und Max Mahlke | Joel Schumacher & Jan Grahe | Christoph Genster, Lisa Schumacher | Sebastian Schaub |
| 12:30 - 13:00 | Barbara Hohenbichler and Rob McNeil | Markus Scheb & Rita Fabry | Daniel Otten und Tobias Hoelzer | Marc Joosten | Theo Glauch und Max Mahlke | Joel Schumacher & Jan Grahe | Christoph Genster, Lisa Schumacher | Sebastian Schaub |
| 13:00 - 13:30 | Barbara Hohenbichler and Rob McNeil | Markus Scheb & Rita Fabry | Daniel Otten und Tobias Hoelzer | Marc Joosten | Christoph Genster, Lisa Schumacher | Sebastian Arnold | Emily Hofmann, Miriam Raths | Lars Poschwatta und Jan Klos |
| 13:30 - 14:00 | Jan Bussmann and Rob McNeil | Markus Scheb & Rita Faby | Daniel Otten und Tobias Hoelzer | Marc Joosten | Christoph Genster, Lisa Schumacher | Sebastian Arnold | Emily Hofmann, Miriam Raths | Lars Poschwatta und Jan Klos |
| 14:00 - 14:30 | Alfred van Munster and Jan Bussmann | Sebastian Wüsten, Sven Just | Sebastian Arnold and Stephan Engels | Emily&Miriam | Christoph Welling | Bernat Terres | Jens Bröder | Christoph Genster, Lisa Schumacher |
| 14:30 - 15:00 | Alfred van Munster and Jan Bussmann | Sebastian Wüsten, Sven Just | Sebastian Arnold and Stephan Engels | Emily&Miriam | Christoph Welling | Bernat Terres | Marion Funken und Lars Mester | Christoph Genster, Lisa Schumacher |
| 15:00 - 15:30 | Alfred van Munster | Sebastian Wüsten, Sven Just | Emily Hofmann, Miriam Raths | Jens Bröder | Lars Poschwatta und Jan Klos | Alexander Epping | Marion Funken und Lars Mester | Christoph Welling |
| 15:30 - 16:00 | Alfred van Munster | Sebastian Wüsten, Sven Just | Emily Hofmann, Miriam Raths | Jens Bröder | Lars Poschwatta und Jan Klos | Alexander Epping | Marion Funken und Lars Mester | Christoph Welling |
Versuchsbeschreibungen / Experiment descriptions
Die anderen Versuchsbeschreibungen folgen.
The other descriptions are coming soon!
Hole in coin (Institute peole only)
The task here is, to get a tiny hole into a coin, without completely destructing it.
To do so, there is various stuff, which could be used.
The solution idea is to freeze a banana with the liquid nitrogen. (This must not be done by the students but by one of the tutors.) Then, the banana can be used as a hammer.
Then, a fixing pin can be sticked into a cork. Now, this can be used as „nail“.
With the banana-hammer, the pin-cork-nail can be used to get a tiny hole into the coin.
To confuse the students a little more, other stuff will be there.
The goal here is, to let the students think about creative solutions for this pretty uncommon probem in style of MacGyver.
There is no need for a final presentation of the „master solution“, because the students may also find no result, which is not too seldom in physics.
Interference with hair (Institute peole only)
The task of this experiment will be to measure the width $ d $ of tiny objects (like hairs) with a monochromatic laser of given wavelength $ \lambda $. To do this, one profits from the fact, that the position of the diffraction minima is the same as in a single-slit experiment whith a slit of the same width $ d $. (Indeed, the basic goal in this experiment is, to understand why.)
A simpe derivation of the corresponding formula $d\,\sin\theta_{n} = n\lambda$ (in Fraunhofer approximation) can be found here: http://en.wikipedia.org/wiki/Diffraction#Single-slit_diffraction
To see, why the minima are at the same positions, consider three systems. First, consider the singe-slit, which we will indicate by $ s $, second, consider the hair ($h$) and finally, consider a free system, where the light ray is propagating without any barrier ($f$).
Let us denote the light's amplitudes on the screen in system $i$ as $A_i(\theta)$. Then, by the principle of superposition,
$A_f(\theta)=A_s(\theta)+A_h(\theta)$.
Assuming the light ray's diameter to be smaller than the position of the first minimum (which can always be gained by moving the screen away from the laser), we have
$A_f(\theta\geq\theta_1)=0$,
because outside the ray, there must be a vanishing amplitude. This implies
$A_h(\theta\geq\theta_1)=-A_s(\theta\geq\theta_1)$.
As what we can see are not amplitudes but intensities $I_i\propto A_i^2$, we can take the square of this equation and get finally
$I_h(\theta\geq\theta_1)\propto I_s(\theta\geq\theta_1)$,
which implies, that the positions of the minima (and indeed, all other critical points) are the same.
This derivation shall be presented to the new students in approximately 5 minutes. If they ask, one should spend another 2 minutes to explain the minima formula for the single-slit.
But the most important thing is to make clear, that we cannot observe the amplitudes directly, but the intensities.
Pendulum
This experiment is probably the one with the biggest part of physics.
The task is to measure Earth's gravity constant $g$ in the usual constant approximation close to the surface.
To do this, the students shall use a pendulum, constructed by a string and some screw nuts.
This system can be approximately described by the differential equation of the harmonic oscillator (Which can be derived by a force ansatz [driving component of gravity] and a Taylor expansion $\sin\varphi\approx\varphi$):
$0=\ddot\varphi+\frac gl \varphi$,
where $\varphi$ is the angle coordinate and $l$ is the length of the pendulum. Of course, this description neglects friction and is ony valid in the usual small-angle approximation.
In this case, the angular frequency $\omega$ is given by
$\omega^2=\frac gl$
which leads to
$g=\omega^2 l$.
(This can for exampe be shown by inserting $\varphi(t)=\hat\varphi\sin{\left(\omega t+\phi\right)}$ into the differential equation.)
The students shall also think about the error on $g$. So, not only the previous part has to be discussed, but also the basic formula for the propagation of errors:
$\sigma_y^2=\sum\limits_i \left(\frac{\partial y}{\partial x_i}\right)^2\sigma_{x_i}^2$
There is no need to derive this formula, but one should present the derivation of the special case of relative errors.
Assuming $y=\prod\limits_i x_i^{\nu_i}$, we have (by the error propagation formula):
$\sigma_y^2=\sum\limits_i \left(\nu_i\cdot x_i^{\nu_i-1}\prod\limits_{j\neq i}x_j^{\nu_j}\right)^2\sigma_{x_i}^2$
Division by $y^2$ then yieds:
$\left(\frac{\sigma_y}y\right)^2=\sum\limits_i \left(\nu_i\cdot \frac{\sigma_{x_i}}{x_i}\right)^2$
With this in mind, the students shall estimate $g$ and $\sigma_g$ as precisely as possible and the shall also think on how to improve their measurement.
For example, a smaller amplitude $\hat\varphi$ leads to a better justification of the small-angle aproximation and measuring $N$ instead of one period reduces the error on the corresponding time $T_N$, which will be dominated by the reaction time of the person who controls the chronograph, by a factor of $\sim N$.
The students shall also think about any other effects that could disturb their measurement. (For example, the string wil not be perfecty rigid and thus, the length $l$ could vary a little bit. And there is also friction!) They shall try to quantify the errors and get a feeling for the dominant ones.
More on the topic can be found here: http://en.wikipedia.org/wiki/Pendulum
The presentation of the differential equation and the related quantities should not take more than 4 minutes. The error propagation formula and the derivation of the relative-error propagation formula could take another 3 minutes.
Balloon rocket
In this experiment, the challenge is, which studentgroup can build the best balloon rocket.
The idea is to bend a balloon to a straw which is fixed on a long cord. Who reaches the furthest point, wins.
The material, the students get, is:
- a balloon per group
- tape
Water rocket
This is just a fun experiment. Some physical backgrounds can be found here: http://en.wikipedia.org/wiki/Water_rocket
It is not neccessary to discuss the whole principle of recoil in a too precise manner. One can give some keywords like:
- The pressure in the water is equivalent to some potential energy.
- When it is allowed to relax (i. e. the mounting is removed), the water will be „shot“ out of the bottle and carry a momentum $p$.
- Due to the principle of momentum conservation, the bottle also has to carry a momentum, namely $-p$.
Apart from this, the students shall have fun and if they wish, they can have a competition on who reaches the biggest shooting distance.
Torricelli's law
The goal of this experiment is to understand Torricelli's law as special case of energy conservation and get a first impression on hydrodynamics. (The final formula can indeed also be derived from Bernoulli's law on hydrodynamics. But it is much more intuitive to new students to use the principle of energy conservation, which they probably feel more familliar with.)
The derivation shall be elaborated together with the students, because they can learn how one could start solving such a problem (in this case, it is conservation of energy) and they can learn the useful „trick“ of virtual displacements.
The system, the students will deal with is a water bottle with three holes of cross-section areas $A_1$, $A_2$ and $A_3$. (The student's task will be to measure those areas.)
Firstly, the students need a relation between the height $h_i (t) $ of the water surface over the $i$th hole and the speed $v_i(t)$ at which the water leaves the $i$th hole. This is given by Torricelli's law:
$v_i(t)=\sqrt{2g h_i(t)}$,
where $g$ is the acceleration caused by Earth's gravity.
Derivation of Torricelli's law from the principle of energy conservation
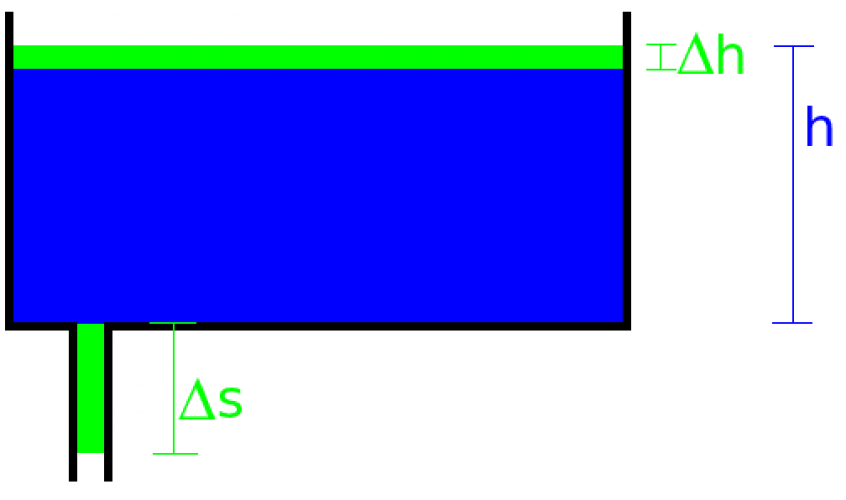
To see this, one can start with a sketch of the system like the following:
We can write the energy $E^i$ of the initial state as:
$E^i=\int\limits_m gh^\prime dm^\prime$,
where $m$ is the whole mass of the water and $dm^\prime$ indicates an integration over every infinitesimal mass element. Note, that we assume no initial dynamics, i. e. no kinetic energy. Via the (constant) mass density $\rho$, we can transform this to an integration over the space, where the water takes place:
$E^i=\int\limits_0^h \rho gh^\prime A(h^\prime) dh^\prime$,
where $A(h^\prime)$ is the cross-sectional area of the infinitesimal water layer at height $h^\prime$ with thickness $dh^\prime$.
In the final configuration (i. e. after an infinitesimal time $\Delta t\to 0$), the energy $E^f$ reads as:
$E^f=\int\limits_{-\Delta s}^{h-\Delta h} \rho gh^\prime A(h^\prime) dh^\prime + \Delta E_{kin}$,
where $\Delta s$ and $\Delta h$ are also infinitesimal and $\Delta E_{kin}$ denotes the kinetic energy of the system. With the infinitesimal volume element $\Delta V$, (which is the water volume that has moved) this kinetic energy can be written as $\Delta E_{kin}=\frac 12 \rho\Delta V v^2$, where $v$ is the speed of the water in the $\Delta s$-regime. (While this regime is infinitesimal, the speed can be seen as constant and there is no need for an integration.)
Then, one finds:
$E^f=\int\limits_{-\Delta s}^{h-\Delta h} \rho gh^\prime A(h^\prime) dh^\prime + \frac 12 \rho\Delta V v^2$
Energy conservation now yields:
$\int\limits_0^h \rho gh^\prime A(h^\prime) dh^\prime=\int\limits_{-\Delta s}^{h-\Delta h} \rho gh^\prime A(h^\prime) dh^\prime + \frac 12 \rho\Delta V v^2$
The equal domains of the integrations now cancel:
$\int\limits_{h-\Delta h}^h \rho gh^\prime A(h^\prime) dh^\prime=\int\limits_{-\Delta s}^0 \rho gh^\prime A(h^\prime) dh^\prime + \frac 12 \rho\Delta V v^2$
As the integration domains, we are left with, will be small, we can approximate the cross-sectional areas as constants $A_h$ and $A_s$, which becomes exact in the final limits $\Delta h, \,\Delta s\to 0$. Then, the integrations can be simplified:
$\rho g A_h \int\limits_{h-\Delta h}^h h^\prime dh^\prime=\rho g A_s \int\limits_{-\Delta s}^0 h^\prime dh^\prime + \frac 12 \rho\Delta V v^2$
Performing this elementary integrations and canceling $\rho$ leads to:
$ \frac 12 g A_h \left[h^2-\left(h-\Delta h\right)^2\right]=-\frac 12 g A_s \Delta s^2 + \frac 12 \Delta V v^2$
Simplifying the bracket and the identity $\Delta V=A_h\Delta h=A_s\Delta s$ yield:
$ \frac 12 g \Delta V \left[2h-\Delta h\right]=-\frac 12 g \Delta V \Delta s + \frac 12 \Delta V v^2$
Canceling $\Delta V$ and then, performing the limits $\Delta h, \Delta s\to 0$ lead to the expression:
$gh=\frac 12 v^2$,
which implies directly Toricelli's law:
$v=\sqrt{2gh}$.
q.e.d.
Measurements
Remember, the goal was, to measure the cross-sectional aereas $A_i$ of the holes in the bottle.
Therefore, one can use the principle of volume flow rate conservation. While water can be seen as incompressible fluid, the total volume flow rate $Q=\dot V$ out of any volume element $\Delta V$ must be $0$, i. e. the flow into any volume element must equal the flow out of this particular volume element.
The volume flow rate through a hole of cross-sectional area $A_h$ can be expressed as
$Q_h=\frac{dV_h}{dt}=A_h \frac{ds}{dt}=A_h\cdot v_h$,
where $dV_h$ be the fluid volume, which passes the hole in the time $dt$, $ds$ be the „way“, the water flows and thus, $v_h$ is the speed of the water.
Thus, the whole volume flow rate through, say, an open bottle with three holes in the wall is
$Q=A_Q \dot h+\sum\limits_{i=1}^3 A_i v_i$,
where $A_Q$ be the (averaged) cross-sectional area of the bottle, $h$ be the height of the water surface, $A_i$ be the cross-sectional area of the $i$th hole and $v_i$ be the speed through it.
Denoting the vertical distance between the water surface and the $i$th hole as $h_i$, one can also write:
$Q=A_Q \dot h+\sqrt{2g}\sum\limits_{i=1}^3 A_i \sqrt{h_i}$
As $A_Q\dot h$ is the water volume $dV$ that leaves the bottle in the time $dt$, one can approximate this quantity directly by measuring the volume $\Delta V$, which leaves the bottle in the (short) time $\Delta t$. Measuring $h_i$ before opening the three holes, one gains the velocities $v_i$.
Note, that $\dot h$ will be negative, because it is associated with a volume flow (of air) into the bottle. Then, one finds:
$\frac{\Delta V}{\Delta t}\approx \sqrt{2g}\sum\limits_{i=1}^3 A_i \sqrt{h_i}$
Now, only the $A_i$ are unknown. Taking three measurements, one can gain a system of three linear equations for the $A_i$, which can finally be solved.
Smart students will start their second measurement, when the first hole is over the water surface and therefore, the sum will reduce to two elements. The third measurement starts, when only the third hole is still under the water surface. (This reduces the efford to solve a system of linear equations, because one already has an upper triangular matrix.
Note, that the measurements shall only start, when the water has no kinetic energy, because otherwise, the derivation conditions for Torricelli's law are not satisfied. Thus, after closing the holes again, one has to wait a moment until the water calms down.
Presentation
This experiment shall give an impression to the new students on how one could start the physical description of a system from first principles. (I. e. conservation laws in most cases.)
Thus, the derivation of Torricelli's law from the principle of energy conservation shall be presented to the students. While this presentation should not take more than approximately 5 minutes, the students shall try to find a proper ansatz and if they do not find it within the first two or three guesses, the principle of energy conservation must be presented as „master solution“
As the students also need to know what to do, one shall give them the ansatz of volume flow rate conservation and show the final formula
$\frac{\Delta V}{\Delta t}\approx \sqrt{2g}\sum\limits_{i=1}^3 A_i \sqrt{h_i} $,
where one shall also make sure, the students know what to do. (Because there will not be much time left.)
While there is no „master solution“ for the cross-sectional areas of the holes, one shall note down the results of all groups to compare them.
Bridge and ship
This is a fun station. The task is to build an bridge over a gap of approximately 50-80cm. To do this, the students get nothing but 10 pages of paper. The winner is the one who builds a bridge on which one can put the most tealights. The second task is to build a ship out of paper which can carry the most tealights. Meanwhile, the ship has to swim on water. Again, the students get nothing but 5 pages of paper. The use of glue or any other aid is forbidden. They may only use for example scissors to cut the paper or some aid to fold it.
Thompson's ring
Another fun experiment.
An electric current $ I $ induces a magnetic field $B$ into a coil.
In front of this coil, there is a metal ring.
Now, Lenz's law yields the induction of another current $I^\prime$ into the metal ring, which is inverse orientated to the original current $I$, i. e. $sgn(I^\prime)=-sgn(I)$.
This leads to another magnetic field $B^\prime$, which causes a strong repusion between the ring and the coil.
Thus, the ring is shot away.
The new students shall try to shoot as far as possible. Note, that one has to take into account kinetic energy of both, tranlation and rotation.
Band generator
This experiment is about having fun with electrostatics.
The new students will get two tasks with a van-de-Graaff band generator. (Additional information can be found here: http://en.wikipedia.org/wiki/Van_de_Graaff_generator)
The voltage for the motor can be varied from $0 V$ up to $\sim 200 V$.
Furthermore, there will be a metal sphere on a metal stick, that shall be connected to earth.
The tasks will be:
- to measure the length of the lightnings as function of the motor voltage
- As many people as possible take each others hands (while they are standing on plastic plates). The first one touches the generator with his second hand. How many people can ruin their hairstyles at the same time?
Do not forget to let everybody touch the earth after the experiment!